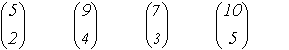|
Se llama factorial de un número natural "n" y se representa por n!, al producto de los números naturales (excluido el 0), menores o iguales que él. |
|
|
n! = n · (n-1) · (n-2) · . . . · 1 |
|
| Para el número 0 esta definición no tiene sentido. Se define el factorial de 0 por 1: 0! = 1 | |
| En la siguiente escena puedes calcular el factorial de cualquier número. | |
|
|
|
|
|
|
Se llama número combinatorio m sobre n a la expresión: |
|
|
|
|
| La siguiente escena te permite calcular cualquier número combinatorio. | |
|
|
|
|
|
|
|
|
|
Hoy en día, con la utilización de la calculadora, es fácil calcular cualquier número combinatorio, sin embargo resulta bastante interesante el cálculo de números combinatorios con el siguiente triángulo, conocido entre otros nombres como Triángulo de Tartaglia, en la que cada número combinatorio se obtiene sumando los dos que tiene encima. En la siguiente escena aparecen las siete primeras filas. |
|
|
 |
|
|
En el triángulo se pueden apreciar algunas propiedades interesantes de los números combinatorios, que se pueden consultar en la siguiente página. |
|