| ESTADÍSTICA |
| Tema
5: Distribuciones Aleatorias |
5.-
CÁLCULO DE PROBABILIDADES EN
UNA
DISTRIBUCIÓN NORMAL.
|
| TIPIFICACIÓN
DE LA VARIABLE |
Para
calcular probabilidades con variables que siguen la
distribución normal se usan tablas. Pero, puesto que
sería imposible tener una tabla para cada posible
distribución normal, solamente la tenemos para la
distribución normal estándar, es decir, para la N( 0 , 1 ).
Necesitaremos,
pues, ser capaces de transformar las variables X
"normales" N(µ,σ) que
encontremos, en variables Z
que sigan una distribución normal estándar N(0,1).
Este proceso de llevar cualquier distribución normal a una N( 0 , 1 ) se llama
"tipificación
de la variable".
Para tipificar X
(o sea, transformarla en Z),
el primer paso es "centrar" la variable; es decir, hacer que la media µ sea 0.
El siguiente paso es conseguir que la desviación
típica σ
sea 1.
Por tanto para tipificar una variable lo que hemos
de hacer es restar la media y dividir por la desviación típica.
| Ejemplo 1: X
→N( 8 , 1.5). Calcula P[ X < 6]
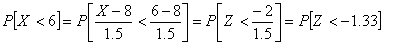 y para
terminar y calcular la probabilidad, aplicamos lo que viene a continuación.
Con esto lo que hemos hecho es simplemente tipificar la variable
transformando la probabilidad pedida en una relacionada con la normal N ( 0
, 1 ). y para
terminar y calcular la probabilidad, aplicamos lo que viene a continuación.
Con esto lo que hemos hecho es simplemente tipificar la variable
transformando la probabilidad pedida en una relacionada con la normal N ( 0
, 1 ).
|
A partir de ahora nos centramos en la
distribución normal N( 0 , 1 ) y vamos a ver cómo calcular probabilidades
en ella. Para distinguir, siempre que hagamos referencia a una variable
N(0,1), vamos a expresarla con la letra Z.
| P [ Z ≤ a ] con
" a " un número positivo |
Un concepto asociado a cualquier distribución de probabilidad es el de Función
de Distribución. La función de distribución en un punto se define como la
probabilidad de que la variable tome valores menores o iguales a él. Así, la
función de distribución en el punto "a", que representaremos por F(a), será :
F(a) = P [ X ≤ a].
| La siguiente escena muestra la función de distribución de
la variable Z → N( 0 , 1 ) para valores positivo de Z. Desplazando
el punto rojo obtienes el valor del área bajo la curva que representa la
probabilidad P [ Z ≤ a ] |
|
|
Calcula las siguientes probabilidades a partir de la escena
y anota los resultados en tu cuaderno:
P [ Z ≤ 0.5]
P [ Z ≤ 1.24]
P[ Z < 2.5 ]
P[ Z < 0 ]
P[ Z ≤ 2.98]
P[ Z ≤ 4]
F( 0.82)
|
Existen tablas de la función de distribución de esta variable N(0,1). A
continuación se muestra la tabla con sus valores.
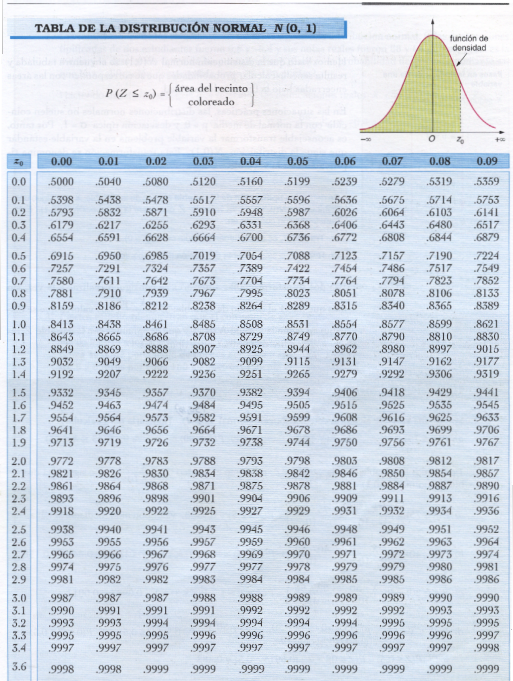
Por ejemplo, si quiero calcular P [ Z ≤ 2.43 ], tenemos que buscar 2.4 en
las filas y 0.03 en las columnas y vemos que en esa cuadrícula lo que aparece es
.9925, por tanto, P [ Z ≤ 2.43 ] = 0.9925
Ejercicio:
Calcula las probabilidades anteriores a partir de la tabla y
comprueba que sale lo mismo que con la escena.
| P [ Z > a ] con
"a " un número positivo |
Aplicando las propiedades de la probabilidad, basta ver que " Z > a" es el
suceso complementario a " Z ≤ a ". Por tanto
P [Z > a ] = 1 -
P [ Z ≤ a ], y esta última la calculamos utilizando las tablas.
Por ejemplo: P[ Z > 1.83 ] = 1 - P [ Z ≤ 1.83 ] = 1 - 0.9664 = 0.0336
P [ Z ≥ 0.49 ] = 1 - P [ Z < 0.49 ] =1 - 0.6879 = 0.3121
|
|
La probabilidad que queremos calcular es la zona coloreada
en celeste.
Modificando el control " valor de -z", observa en la escena de
la izquierda que en cada momento, la zona celeste es igual a la zona
amarilla
debido a la simetría de la distribución normal y por tanto P[ Z < -
a ] = P [ Z > a ]
En la parte de la derecha puedes ver lo que hemos comentado
anteriormente, la zona amarilla es igual a
1 - zona verde que es lo que
aparece en las tablas.
Por tanto, P[ Z < -a ] = P [ Z > a ] = 1 - P [ Z ≤ a ]
P [ Z < - a ] = 1 - P [ Z ≤
a]
|
Ejemplo : P [ Z ≤ -1.37 ] = P [ Z > 1.37] = 1 - P [ Z ≤
1.37] = 1- 0.9147 = 0.0853
P [ Z < -0.04] = 1 - P [ Z < 0.04 ] = 1- 0.5160 = 0.484
Aplicando las propiedades de la probabilidad, tenemos que: P [ Z > - a] =
1 - P [ Z ≤ - a ] = 1 - ( 1 - P [ Z < a ] ) = P [ Z < a ].
Luego P [ Z > -a] = P [ Z < a ].
Ejemplo : P [ Z ≥ - 1.14] = P [ Z < 1.14] = 0.8729
P [ Z > -3] = P [ Z < 3 ] = 0.9987
| Probabilidad en un
intervalo; P [ a < Z < b ] |
|
|
Vamos a ver ahora cómo calcular probabilidades de intervalos
(z1, z2); es decir, P(z1<Z<z 2).
Queremos calcular la probabilidad del intervalo (z1,
z2), que está marcada en la figura B, pero en la tabla
sólo aparecen probabilidades del tipo: P(Z
≤
z 0)
Dale distintos valores a z1 y a z2
y observa los gráficos. Busca la manera de calcular la probabilidad
P(z1≤ Z ≤z2) a partir
de las probabilidades
que conocemos P(Z
≤ z0 )
|
P [ a < Z < b ] = P [ Z < b] - P [ Z < a ]
|
EJERCICIOS
|
| |
1. Sea Z una variable aleatoria
que sigue una distribución N (0 , 1 ). Halla las siguientes
probabilidades:
- P(Z ≥ 0.32)
- P(Z ≤ 0)
- P ( Z > 0.7 )
- P ( -0.51 ≤ Z ≤
0.51)
- P [ Z ≤ - 1.45 ]
- P [ Z > - 2.63]
|
| |
2. En una distribución normal
N ( 5, 2 ) calcula las siguientes probabilidades:
- P ( X ≤ 3.25)
- P [ X > 4.5 ]
- P [X ≤ 7.2]
- P [ 3 < X ≤ 6]
|
| |
|
| |
|
3. El tiempo necesario para que
una ambulancia llegue a un centro sanitario se distribuye según una variable
normal de media 17 minutos y desviación típica 3 minutos. Calcula la
probabilidad de que el tiempo de llegada esté comprendido entre 13 y 21
minutos. ¿Cuánto tiempo se espera que tarde la ambulancia en llegar? ¿ Para
qué valor de t, la probabilidad de que el tiempo de llegada sea superior a t
es del 5%? |
|
|
|
4. Un estudio antropológico de
una tribu del centro de África ha constatado que la longitud del dedo
corazón de los adultos sigue una ley normal de media 60 mm y varianza 9 mm.
Si hay 800 adultos en esa tribu, determina cuántos tienen el dedo corazón:
a) Más largo de 62
mm
b) Más corto de 57
mm.
c) Entre 60 y 66 mm.
|
|
|
5.El peso teórico de la tableta
de cierto medicamento es de 234 mg. Si suponemos que los pesos de la
tabletas tienen una desviación típica de 10 mg por tableta y que se
distribuyen normalmente,
- ¿Cuál será el tanto
por ciento de tabletas con peso menor o igual a 210 mg?
- ¿Cuál será el tanto
por ciento de tabletas con peso superior a 240 mg?
|
|
|
|
6.El tiempo de vida de una
bombilla sigue una distribución normal N(180, 15), donde el tiempo se mide
en horas. ¿Cuál es la probabilidad de que al comprar una bombilla, luzca más
de 195 horas? ¿ Y menos de 170? |
|
|
|
7. Un laboratorio farmacéutico
prepara pastillas circulares con un diámetro medio de 12 mm y una desviación
típica de 0,8 mm, pero si la pastilla fabricada tiene un diámetro inferior a
9.5 mm o superior a 14.7 mm, ésta se rechaza por no tener la cantidad
adecuada de medicamento. Sabemos además que el diámetro sigue una
distribución normal. ¿Cuál es la probabilidad de que al fabricar una
pastilla, ésta esté en condiciones de ser utilizada? |
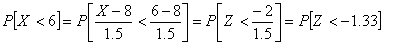 y para
terminar y calcular la probabilidad, aplicamos lo que viene a continuación.
Con esto lo que hemos hecho es simplemente tipificar la variable
transformando la probabilidad pedida en una relacionada con la normal N ( 0
, 1 ).
y para
terminar y calcular la probabilidad, aplicamos lo que viene a continuación.
Con esto lo que hemos hecho es simplemente tipificar la variable
transformando la probabilidad pedida en una relacionada con la normal N ( 0
, 1 ). 



