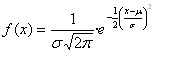
| ESTADÍSTICA |
| Tema 5: Distribuciones Aleatorias |
4.- VARIABLES ALEATORIAS CONTINUAS. LA DISTRIBUCIÓN NORMAL. |
| FUNCIÓN DE PROBABILIDAD DE UNA VARIABLES ALEATORIAS CONTINUA |
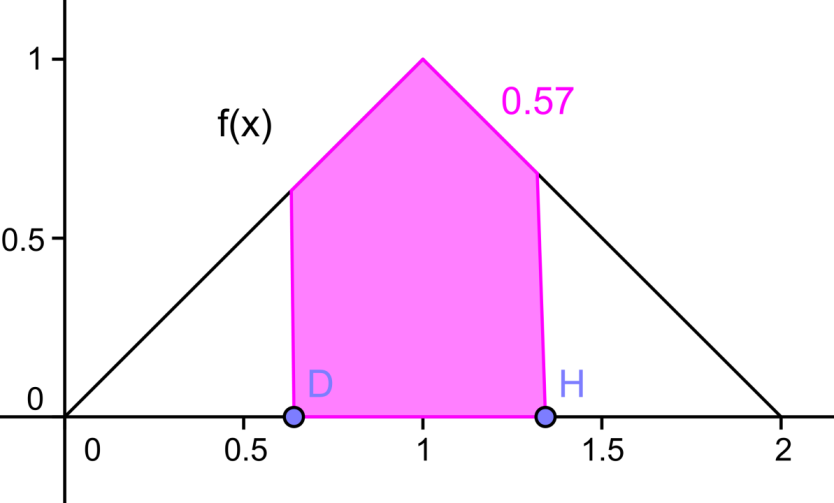 Si queremos calcular la probabilidad de X Tome valores entre los Puntos
D y H, tendríamos que calcular el área bajo la curva entre los puntos D
y H, es decir la el área sombreada con color rosa. Así pues, P[ D <
X < H ] = "área rosa" = 0.57.
Si queremos calcular la probabilidad de X Tome valores entre los Puntos
D y H, tendríamos que calcular el área bajo la curva entre los puntos D
y H, es decir la el área sombreada con color rosa. Así pues, P[ D <
X < H ] = "área rosa" = 0.57.|
En esta escena se representa el histograma de frecuencia relativa de una variable continua. |
||
1.- Con el valor de los controles iniciales se representa un histograma para 1000 valores agrupados en 25 intervalos. 2.- La variable que estudiamos depende de muchos factores independientes y su media es aproximadamente igual a 100. 3.- Aumenta el control 'nº de puntos' y observa el histograma. 4.- El modelo al que tiende es un histograma simétrico centrado en una media igual a 100. 5.- Para ver la función de densidad dale el valor '1' al control Responde en tu cuaderno a las siguientes cuestiones:
|
||
Propiedades de las distribuciones continuas
Por tanto en una distribución continua, no existe diferencia entre los
símbolos < y ≤ ni entre los símbolos > y ≥.
| LA DISTRIBUCIÓN NORMAL |
Pues bien, una variable aleatoria continua decimos que sigue una distribución normal de parámetros µ y σ, ( X →N( µ, σ ) ) si su función de densidad asociada viene dada por
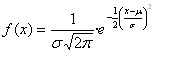
La gráfica de esa función recibe el nombre de curva o campana de
Gauss, debido al aspecto que presenta y en la siguiente escena la puedes
observar
|
En esta escena representa la función de densidad de una distribución normal de media cero y desviación típica uno. La llamaremos N(0,1). A la variable se la denomina 'z'. Vamos a estudiar las propiedades de la función de densidad obtenida en la escena anterior. Responde a las siguientes cuestiones: |
|
|
1.- Con 'comenzar=0' dale distintos valores a la media y observa cómo cambia la función. Haz lo mismo con la 'desv típ'. 2.- Cuando has variado los controles anteriores, ¿para qué valor de la variable alcanza siempre el máximo la función? 4.- La probabilidad de que la variable se encuentre entre dos valores viene dada por el área bajo la curva. Dale a 'comenzar' el valor 1 y lo verás mejor. Mueve los controles, manteniendo P a la izquierda de Q y verás el área ( zona coloreada), es decir la probabilidad de que la variable se encuentre entre los dos números representados en el eje de abscisas.
5.- Si X es N(1.8 , 2.2), calcula: P[-2<X<3]; P[X≥ 0 ] y P[X < 5] *utiliza el zoom si es preciso. 6.- Si X es N(-1.3 , 0.5 ) , calcula: P [ X > -1]; P [ 0.5 < x ≤ 1.5 ]
|
|
 |
 |
 |
 |