Distribución Binomial

ESTADÍSTICA

Tema 5: Distribuciones Aleatorias

3.- LA DISTRIBUCIÓN BINOMIAL

Supongamos que un experimento aleatorio tiene las siguientes características:

El experimento aleatorio consiste en repetir un cierto número de veces, "n", una determinada prueba.
En cada prueba del experimento, sólo son posibles dos resultados: el suceso A, que llamaremos éxito y su complementario, llamado fracaso.
El resultado de cada prueba es independiente de los resultados obtenidos anteriormente, es decir, el resultado obtenido en la primera prueba, no influye para nada en el posible resultado de la segunda o la tercera.
La probabilidad de que ocurra el éxito es siempre la misma y la expresaremos como "p", y por tanto, la probabilidad de fracaso será q = 1 - p .

Todo experimento aleatorio con estas características se dice que sigue el modelo de la distribución binomial, y a la variable X que expresa el número de éxitos obtenidos en las n repeticiones de la prueba, se le llama variable aleatoria binomial y se representa por
B( n , p ); donde "n" es el número de repeticiones de la prueba y "p" la probabilidad de éxito.

Ejemplos de variables que siguen una distribución binomial:

Número de caras al lanzar 7 monedas.
Número de piezas defectuosas que fabrica una máquina.
Número de chinchetas que al caer quedan de punta.

En esta escena se representa la función de probabilidad una distribución binomial B(n,p).

Características de una B(n,p):

a.- Repetimos n veces un experimento y se considera si se verifica o no un determinado suceso.

b.- La probabilidad de que se verifique dicho suceso se mantiene constante y la llamamos p.

c.- Las pruebas son independientes unas de otras.

d.- La variable X es el número de veces que se verifica dicho suceso y está comprendido entre 0 y n

e.- En el eje OX se representan los valores de X y en último paso su probabilidad.

Pinchando sobre el botón paso, verás en primer lugar la representación gráfica de la función de probabilidad de la variable y después los valores de esas probabilidades.

Comprueba en la escena que se cumplen las siguientes afirmaciones:

Si p=0.5, la distribución de probabilidad es simétrica.
Si p está próximo a cero, los valores pequeños tienen probabilidad alta y lo mayores tienen probabilidad prácticamente 0. Es decir, la distribución está tirada a la izquierda.
Si p está próximo a 1, ocurre todo lo contrario que en el punto anterior.
Comprueba que los tres puntos anteriores se cumplen sea cual sea el valor de n.
Una máquina fabrica piezas defectuosas con una probabilidad de 0,05. Calcula la probabilidad de que al fabricar 20 piezas 6 seis sean defectuosas.¿Y de que sean 3 las defectuosas?¿Y que todas sean buenas?

Veamos cómo calcular la probabilidad de los distintos valores de X con un ejemplo:
"Un examen tipo test consta de 10 preguntas, cada una de ellas con tres posibles respuestas, de forma que sólo una de las tres es correcta. ¿Cuál es la probabilidad de que un estudiante que contesta al azar acierte 6?"

Definimos X="Número de aciertos en las 10 preguntas". En este caso, cada pregunta es cada una de las pruebas que se repiten, o sea, n = 10.
De la manera que está planteado el problema sólo hay dos posibles resultados, o acierta (éxito, pues me preguntan sobre los aciertos) o no acierta (fracaso) y la probabilidad de acierto en cada prueba es la misma, 1 / 3.

Por tanto efectivamente X sigue una distribución binomial ; X es B(10, 1/3) y el problema me pide P [ X = 6 ]

Para calcular esa probabilidad, observamos que X = 6 significa 6 aciertos y 4 fallos, o sea (1 / 3 ) ⁶ · (2 / 3 ) ⁴. Además hay que tener en cuenta cómo repartir los 6 acierto a lo largo de las 10 preguntas; no importa el orden y no se pueden repetir las preguntas, por tanto combinación sin repetición de 10 elementos tomados de 6 en 6.Luego la probabilidad pedida es:

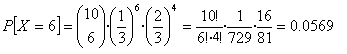
En general, si X sigue una distribución B(n , p ), la función de probabilidad viene dada por la fórmula: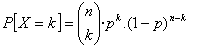

Parámetros de una distribución binomial:

El cálculo de la media y la varianza de una distribución binomial es inmediato si conocemos sus parámetros n y p. Haciendo cálculos se llega a que:

Esperanza: E(X) = n·p
Varianza: Var(X) = n·p·q; donde q = 1- p, o sea, la probabilidad de fracaso.

Ejercicios
*Todos los ejercicios hay que empezarlos definiendo una variable y relacionando la probabilidad pedida con valores de la variable.

1.- La probabilidad de que una pieza fabricada por una empresa sea defectuosa es 0.1. Halla la probabilidad de que en una muestra de 100 piezas se encuentren tres defectuosas.

2.- La probabilidad de que un estudiante de primero de la licenciatura de física obtenga el título es de 0.2. Halla la probabilidad de que en un grupo de 8 alumnos de primer curso, al menos dos acaben la carrera. ¿Cuál es la probabilidad de que no lo acabe ninguno?

3.- El 60% de los licenciados de una facultad encuentran trabajo el primer año después de acabar la carrera. De los 150 licenciados en un curso, ¿cuántos se espera que se coloque en el primer año? ¿Cuál es la desviación típica?

4.- Un laboratorio ha comprobado que el 25% de los que toman un determinado antibiótico sufren efectos secundarios. De una muestra de ocho enfermos que toman dicho antibiótico, halla la probabilidad de que sufran efectos secundarios:

Al menos seis
Más de dos
Menos de la mitad
A lo más 3
Todos
Halla el número de enfermos esperado con efectos secundarios.

5.- Suponiendo que el 43% de los españoles tengan Rh^-, si tomamos una muestra de siete personas, ¿qué probabilidad hay de que todas sean Rh^-? ¿Y de que cuatro sean Rh⁺ ?