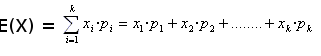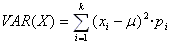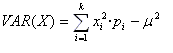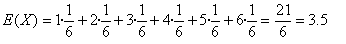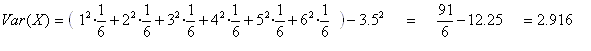ESTADÍSTICA
Tema 5: Distribuciones Aleatorias


1.- VARIABLES   ALEATORIAS  DISCRETAS

Una variable aleatoria se dirá discreta si el conjunto de valores que toma es un conjunto numerable, es decir, que solo puede tomar unos valores concretos. Dicho conjunto lo denotaremos por: {x1, x2, x3,...., xk}

Toda variable aleatoria discreta tiene asociada una función de probabilidad, que a cada valor, le marca la probabilidad de que la variable tome  dicho valor. Esta probabilidad viene a jugar el mismo papel que la frecuencia relativa en los temas de estadística.
Ejemplo 1: Obtener la función de probabilidad de la variable "puntuación obtenida al lanzar un dado".

Definimos la variable aleatoria X= puntuación obtenida.
Los posibles resultados son: 1, 2, 3, 4, 5 y 6  y todos esos valores tienen una probabilidad de 1 / 6.
Si ponemos en forma de tabla los resultados, la función de probabilidad quedaría:
Valores de la varible  xi Función de Probabilidad
 pi =  P[X = xi]
1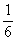
2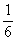
3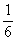
4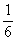
5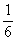
6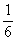

Ejemplo 2:  Obtener la función de probabilidad de la variable "número de caras obtenidas al lanzar tres monedas"

Antes que nada, vamos al construir el espacio muestral del experimento lanzar tres monedas. Éste sería:
E = {(c,c,c); (c,x,c); (x,c,c); (c,c,x); (c,x,x,); (x,c,x); (x,x,c); (x,x,x)}
Si definimos X = nº de caras obtenidas, vemos que los posibles valores son: 0, 1, 2 y 3; y la función de probabilidad será:
xi 0 1 2 3
pi 1/8 = 0.125 3/8 = 0.375 3/8 = 0.375 1/8 = 0.125

Como puedes observar en los dos ejemplos, la suma de todas las probabilidades tiene que ser 1, pues estaríamos considerando el espacio muestral completo.


Parámetros de una variable aleatoria
La ventaja de trabajar con variables aleatorias es que podemos hacer cálculos que adquieren signifcado sobre el comportamiento de la variable. En una variable aleatoria, podemos calcular todos los parámetros que habíamos visto en la estadística unidimensional: media, varianza moda, mediana, percentiles, desviaciones, etc, aunque nosotros vamos a centrarnos en las dos primeras, la media y la varianza, (bueno o la desviación típica que era la raíz de la varianza si recuerdas)

MEDIA: La media de una variable aleatoria se llama ESPERANZA  MATEMÁTICA, se representa por  E(X) o por µ  y viene a darnos el "valor esperado" de la variable al realizar el experimento aleatorio.  La fórmula para calcularla es
  esperanza matemática

VARIANZA:  El significado es el mismo que en la estadística. Aporta una medida sobre la dispersión de los valores de X. Para calcularla usamos una de las dos fórmulas, aunque es más aconsejable la segunda:
varianza                varianza
Veamos un par de ejemplo:


Ejemplo: Calcula la media y la varianza de la variable del Ejemplo 1
  xi  
 pi =  P[X = xi]
1
2
3
4
5
6
 
Lo que significa que el valor esperado en el lanzamiento de un dado es 3,5


y si queremos calcular la desviación típica, haríamos la raíz cuadrada de ese resultado y obtendríamos, 1.708

Ejemplo : Calcula la esperanza y la varianza de la variable  número de caras del ejemplo 2

xi 0 1 2 3
pi 1/8 = 0.125 3/8 = 0.375 3/8 = 0.375 1/8 = 0.125
E(X) =0·0,125  +  1·0,375  +  2·0,375  +  3·0,125  =  1,5. Luego el número de caras esperado en el lanzamiento de tres monedas es una y media.
Var (X) =(02·0,125  +  12·0,375  + 2 2·0,375  +  32·0,125 )  -  1.52  =  
 = 3 - 2.25  =  0.75


Ejercicios
1.- En la siguiente tabla se presenta la distribución del número de hijos de un grupo de 100 parejas:
Nº de hijos 0 1 2 3 4 5 7
Nº de parejas 15 40 23 10 7 4 1

  1. Obtener la función de probabilidad de la variable aleatoria nº de hijos
  2. ¿Cuál es la probabilidad de una pareja elegida al azar tenga menos de dos hijos?
  3. ¿Cuál es la probabilidad de que tenga más de tres hijos?
  4. Si se elige un hijo al azar, ¿cuál es la probabilidad de que no tenga hermanos?
  5. Determina el número de hijos esperado al selecionar una familia al azar.
  6. Calcula la varianza de la variable.
2.- Una variable aleatoria discreta tiene la siguiente función de probabilidad:
Xi -2 -1 0 1 2 3
pi 0.08 0.21 0.1 0.23 0.04

  1. Calcula el dato que falta.
  2. Halla la media y la desviación típica.
  3. Calcula P[X > 1]  y   P[ -1.5 < X < 2]
3.- ¿Cuál es el dinero que espera ganar un jugador que lanza dos dados de quinielas ( o sea, solo con tres caras, 1, X y 2)  y recibe 90 € si salen dos doses; 45 € si sale un dos y paga 81 € si no sale dos?
4.- Utilizando variables aleatorias, hacer un estudio comparativo y ver que  interesa más; echar 4 quinielas ( a 0.50 € la apuesta), echar 2 primitivas ( a 1 € la apuesta) o echar un euromillones ( a 2 € la apuesta)
Usar una hoja de cálculo en la que para cada apuesta poner en una columna los premios, en otro el dinero que reporta y en otra la probabilidad. Interesará más, la que más nos aporte por término medio.


Índice