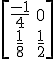
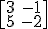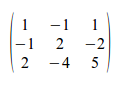5. Matriz inversa
Importante
 |
| Imagen de German Adolfo bajo licencia Creative Commons |
La inversa de una matriz A, que representaremos por A-1, es otra matriz de la misma dimensión y que cumple que al multiplicarla por ella da la identidad del orden que le corresponda:
A·A-1 = I y A-1·A = I
Puesto que las dos matrices tienen la misma dimensión, para que el producto se pueda hacer, la matriz A tiene que ser cuadrada. Es decir, la inversa de una matriz sólo tiene sentido para matrices cuadradas.
Luego en nuestro ejemplo no se podría hacer.
La matriz inversa no siempre existe, para que exista, es condición necesaria y suficiente que el determinante de la matriz sea distinto de cero:
![]()
Inversa por el método de Gauss
Bueno, pues vamos a ver cómo se hace esto de la matriz inversa. ¿Recuerdas del curso pasado el método de Gauss para resolver un sistema de ecuaciones con tres incógnitas? Básicamente había que hacer ceros por debajo de la diagonal multiplicando las filas por números y sumándolas.
Pues algo similar vamos a hacer aquí. Este es el método de Gauss-Jordan.
Applet Descartes de Alfredo Pena Iglesias bajo licencia Creative Commons.
Si no te ha quedado muy claro, con el siguiente vídeo seguro que sí:
Inversa por Determinantes
La formula con la que se calcula la matriz inversa es:
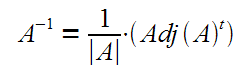
En estos vídeos puedes ver cómo se calcula la matriz inversa aplicando esta fórmula, primero para una matriz 2x2 y después para una de orden 3x3:
| Inversa matriz orden 2 |
Inversa matriz orden 3 |
Curiosidad
PROPIEDADES DE LA MATRIZ INVERSA
1. La matriz inversa si existe es única.
2. (A-1)-1 = A, es decir, la inversa de la inversa es la matriz inicial.
3. (A·B)-1 = B-1·A-1
4. |A-1| = 1 / |A|
 |
| Imagen de El Matenavegante bajo licencia Creative Commons |
Te proponemos cuatro matrices para que practiques:
1) 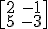
2) 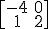
3) 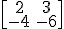
4) 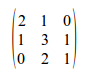
Siguiendo el enlace, puedes hacer ejercicios de calcular matrices inversas: