Resolución de Problemas
En esta página se muestran ejemplos de ejercicios y problemas resueltos, relacionados con los contenidos de la unidad. En mayor o menor medida se abordan todos los tipos de ejercicios y problemas que se pueden hacer.
Nota: Todas las operaciones están redondeadas con dos o tres decimales.
EJERCICIO 1: Calcula las razones trigonométricas del ángulo α :
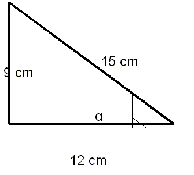
Como ves, los tres lados del triángulo son conocidos, así que para calcular las razones trigonométricas sólo tenemos que aplicar las fórmulas y sustituir. Para el ángulo α el cateo opuesto es 9, el contiguo 12 y la hipotenusa 15.
EJERCICIO 2: Calcula las razones trigonométricas del ángulo C del siguiente triángulo
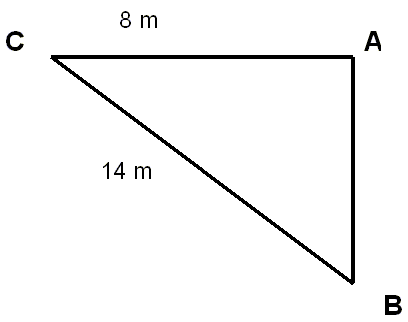
Ahora en este ejercicio ya no tenemos los tres lados, falta uno de los catetos y para calcularlo vamos a utilizar el Teorema de Pitágoras.
Lo primero ponerle nombre a los lados. Vamos a llamarle con letras minúsculas a los lados que están enfrente del ángulo con la correspondiente letra mayúscula; es decir a = 14 m, b = 8 m y c es el lado que queremos calcular
Aplicando el Teorema de Pitágoras tenemos:
a2 = b2
+ c 2
142= 82
+ c2
196 = 64 + c2
196 - 64 = c2
132 = c2
y aplicando las fórmulas
11,49 = c
tenemos:
Luego c = 11, 49 m.
EJERCICIO 3: Determina los ángulos del ejercicio anterior
Obviamente ya sabemos que el ángulo A es el ángulo recto y por tanto A = 90º. Para calcular los otros dos vamos a hacerlo con las razones trigonométricas y con la ayuda de la calculadora.
Si queremos calcular el ángulo C con los datos que parto, lo primero es identificar los lados que conozco respecto al ángulo C, que en este caso son cateto contiguo e hipotenusa y pienso en qué razón trigonométrica intervienen esos lados. La respuesta es el coseno, así que calculo cos C
Cos C = 8 / 14 = 0,57. Ahora con la calculadora sacamos cuál es el ángulo, utilizando la función inversa de la tecla "cos", y el resultado es C = 55,25º.
Para calcular B puedo hacer lo mismo, pensar qué razón puedo calcular, o como ya tengo dos ángulos, sacarlo de que la suma de los ángulos de cualquier triángulo es 180º ( A + B + C = 180). Por cualquier camino el resultado es B = 34,75º.
EJERCICIO 4: De un triángulo rectángulo se sabe que uno de sus ángulo agudos es 40º y que el cateto opuesto a éste mide 10m. Calcula el ángulo y los lados que faltan.
Lo primero es hacer un dibujo que nos aclare la situación y ponerle nombre a los lados y ángulos
Esta sería nuestra situación.
Para empezar los más fácil es sacar el ángulo que falta, y aplicando que la suma de los tres es 180, el ángulo B vale 50º.
Vamos a calcular ahora por ejemplo el lado "b". Si me fijo en el ángulo C, el lado que sé es el cateto opuesto y el que pretendo calcular es el contiguo. Como la razón trigonométrica en la que intervienen estos es la tangente, voy a calcularla con la calculadora y despejar a partir de ahí:
Por tanto ya tenemos el lado "b". Para calcular
el lado "a" podríamos aplicar Pitágoras o sacarlo por alguna razón. Vamos a
seguir este camino que será más corto.
Por ejemplo voy a fijarme en el lado "c" y
el ángulo "C", aunque ya podría utilizar cualquiera de los datos que tengo. Para
el ángulo "C" sé cateto opuesto y quiero hipotenusa; así que habrá que utilizar
el seno:
EJERCICIO 5: Calcula
la altura de la torre si nuestro personaje está a 7 m de la base de la
torre,
el ángulo con el que está observando la cúspide es de 60º y sostiene el artilugio
a una altura de 1,5 m.
Para comenzar, vamos a hacer un dibujo
que
aclare un poco la situación poniendo los datos que conocemos.
Si nos fijamos en el triángulo, el lado c mide 7 m y una vez que tengamos calculado el lado b, para calcular la altura de la torre sólo tendremos que sumarle los 1,5 m. Así pues, vamos a calcular el lado b.
Para el ángulo 60º, el lado que conozco es el cateto contiguo y el que quiero calcular es el cateto opuesto, así pues planteo la tangente de 60º.
Por tanto la altura de la torre es 12,11 m + 1,5 m = 13, 61 m.
EJERCICIO 6: El seno de cierto ángulo α del segundo cuadrante vale 0,45. Calcula el coseno y la tangente.
Para resolver este ejercicio tenemos que recurrir a las relaciones trigonométricas. De la primera sacaremos el valor del coseno y una vez que lo tengamos sacaremos la tangente:
Sacamos el valor del coseno despejándolo de la fórmula: sen2α + cos2α = 1.
Como nuestro ángulo está en el segundo cuadrante y en ese cuadrante el coseno es negativo, tenemos que quedarnos con el signo -, por tanto cos α = - 0,893.
Para calcular el valor de la tangente, aplicamos
la segunda fórmula:
EJERCICIO 7:
Sabiendo que cos 42º = 0,74. Calcula:
sen 222º, tg
138º, cos 48º, sen 318º y sen 132º.
sen 222º
El ángulo 222º pertenece al tercer cuadrante.
Vamos a ver con que ángulo del primero se relaciona: α = 222º - 180º = 42º.
Por
tanto y teniendo en cuenta que el seno en el tercer cuadrante es negativo,
sen222º = - sen 42º = - 0,669 (Para
calcular el sen 42º seguimos el mismo procedimiento que en el ejercicio 6).
tg 138º
138º está en el segundo cuadrante y se relaciona
del primero con α = 180º - 138º = 42º, que vuelve a ser el ángulo que conocemos.
Como la tangente es negativa en el segundo cuadrante, tg 138º= - tg 42º= -0,9
(tg 42º lo calculamos igual que en el ejercicio
6)
cos 48º
48º es del primer cuadrante, pero cumple que es
el complementario del ángulo que conozco 42º.
Entonces cos 48º = sen 42º = 0,669.
sen 318º
318º está en el cuarto cuadrante y se relaciona
con 360º - 318º = 42.
Entonces sen 318 º= - sen 42º = - 0,669
sen132º
132º es del segundo y se relaciona con 180º - 132º =
48º que es el complementario de 42º.
Entonces y como el seno es positivo en el
segundo cuadrante, sen 132º = sen 48º = cos 42º = 0,74.
Ahora te toca ti. Pincha en el menú en el apartado "Ejercicios" , accede a los ejercicios propuestos y comprueba lo que has aprendido.
