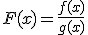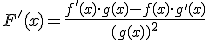2.2. Reglas de derivación
Importante
| Operación |
Función |
Derivada |
| Producto por una constante |
F(x)= a·f(x) | F '(x)=a·f '(x) |
| Suma o resta |
F(x) = f(x) + g(x) |
F'(x) = f'(x) + g'(x) |
| Producto de funciones |
F(x) = f(x)·g(x) | F'(x) = f'(x)·g(x) + f(x)·g'(x) |
| Cociente de funciones |
|
|
Ejemplos
| Derivada de un monomio |
Derivada de un polinomio |
|
|
|
| Derivada de un producto |
Derivada de un cociente |
|
|
|
Autoevaluación
En este enlace puedes practicar con derivadas sencillas como las que llevamos hasta ahora.
Importante
Regla de la cadena
Para derivar una función compuesta, utilizamos la llamada regla de cadena, que consiste en ir derivando cada función que nos vamos encontrando respetando su argumento y multiplicando por la derivada de ese argumento:
f(g(x))' = f '(g(x))·g'(x)
A continuación varios ejemplos
Ejemplos
| Un polinomio elevado a una potencia |
Cociente con potencia |
| Seno y exponencial |
Coseno con potencias dentro y fuera |
| Logaritmo, potencia y cociente | Arcotangente, seno y potencia |
Autoevaluación
En este enlace, ejercicios de derivadas para practicar aplicando la regla de la cadena