5. Aplicaciones de las derivadas al cálculo de límites
Importante
Regla de L´Hôpital
Sean f y g dos funciones continuas que cumplen que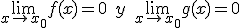 
, es decir, que el límite 
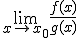nos da una indeterminación 0/0.
Si además cumplen que existen f '(x) y g '(x) en un entorno de x0, entonces se puede afirmar que:
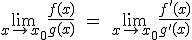
Esta regla también es válida sin en lugar de hacer el límite en un punto se hace en +∞ o -∞, o si el resultado de los límites de f y g es en ambos casos infintio, es decir, si tenemos la indeterminación ∞/∞.
Ejemplos resueltos
Podemos resolver cualquier indeterminación con esta regla, siempre que la transformemos en 0/0 o ∞/∞ y las funciones del numerador y del denominador sean derivables donde estamos calculando esos límites.
A continuación, cuatro ejemplos de cálculo de límites usando la regla de L´Hôpital:
| 0/0 con senos y cosenos |
0/0 con coseno y exponencial |
| 0 por infinito |
infinito menos infinito |