6. Sistemas de ecuaciones lineales
Importante
Los sistemas de ecuaciones se clasifican o se distinguen según el número de soluciones que tengan. Así tenemos:
- Sistema Compatible Determinado (SCD), cuando tiene una única solución.
- Sistema Compatible indeterminado (SCI), cuando hay infinitas soluciones, soluciones que dependerán de uno ovarios parámetros.
- Sistema Incompatible (SI), si no hay solución.
El Teorema de Rouché-Fröbenius nos aporta un método para saber cómo es un sistema de ecuaciones lineales, sin necesidad de resolverlo, a partir del rango de las matrices de coeficientes y ampliada.
De forma resumida, este teorema nos dice que:
Si el rango de la matriz de coeficientes es igual al rango de la matriz ampliada y además igual al número de incógnitas, el sistema es compatible determinado.
Rang(A) = Rang(A*) = n.º incógnita → SCD
Si el rango de la matriz de coeficientes es igual al rango de la matriz ampliada pero menor que el número de incógnitas, el sistema es compatible indeterminado.
Rang(A) = Rang(A*) < n.º incógnita → SCI
Por último, si los rangos de las matrices de coeficientes y ampliada son distintos, el sistema es compatible indeterminado.
Rang(A) < Rang(A*) → SI
Ejemplo o ejercicio resuelto
En este vídeo te mostramos cómo se discute un sistema de ecuaciones lineales que depende de un parámetro:
Curiosidad
 |
| Imagen de craigCloutier bajo licencia Creative Commons |
Un sistema se dice que es homogéneo si todos sus términos independientes son ceros. Por ejemplo, el sistema que ponemos a continuación es homogéneo:
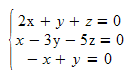
Pues bien, estos sistemas siempre son compatibles, pues al hacer la matriz ampliada añadimos una columna de ceros, por lo que el rango no puede aumentar, así que, en estos sistemas, siempre habrá solución, una ( que será (0,0,0) ) o muchas según sea compatible determinado o indeterminado.