1. La idea intuitiva de límite
Fíjate en la siguiente escena. Pulsa sobre el botón "play" y observa la secuencia que hace la gráfica para acercarse a 0. Esa secuencia es la que debes recorrer tú cuando quieras calcular un límite.
Applet Descartes de José Manuel Gallardo Morilla bajo licencia Creative Commons.
Observa ahora esta escena. Haz lo mismo, pulsa sobre el botón "play" y observa lo que ocurre en la gráfica cuando nos acercamos a 0 en el eje X.
Applet Descartes de José Manuel Gallardo Morilla bajo licencia Creative Commons.
Esta función es una de las que has visto en el tema anterior y en el curso pasado, una función a trozos que se está cortando en 0, y fíjate que según por el lado que nos acerquemos a cero, la función se acerca a un valor u otro. Si lo hacemos por la izquierda, la función se acerca a -1, mientras que si lo hacemos por la derecha, los valores de la función se aproximan a 1.
Por tanto, es necesario indicar por qué lado nos estamos acercando al punto, y surge así el concepto de límite lateral.
- Se llama límite lateral por la izquierda de la función f en el punto x0,al valor al que tiende la función cuando los valores de x que se aproximan a x0 son menores que x0. Lo expresamos con un signo - sobre el punto así:
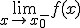
En el ejemplo,
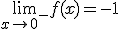
- Se llama límite lateral por la derecha de la función f en el punto x0,al valor al que tiende la función cuando los valores de x que se aproximan a x0 son mayores que x0. Lo expresamos con un signo + sobre el punto así:
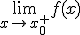
En el
ejemplo,
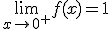
- El límite de una función en un punto existe si los dos límites laterales existen y coinciden. Así, en el ejemplo, el límite en 0 no existiría al no coincidir los límites laterales.
Calcula los siguientes límites a partir de esta gráfica. En caso de no existir escribe no
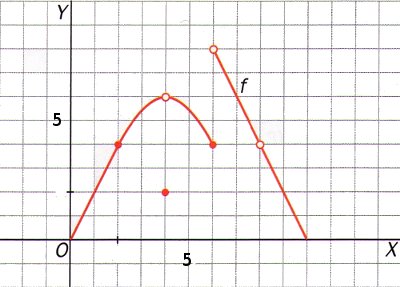
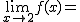
|
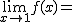
|
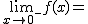
|
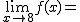
|
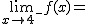
|
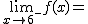
|
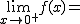
|
f(8)= |
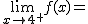
|
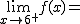
|
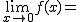
|
f(4)= |
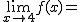
|
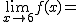
|
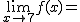
|
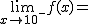
|
 |
| Imagen de viernest bajo licencia Creative Commons |
Pero claro, como comprenderás no siempre disponemos de la gráfica de la función, sino que muchas veces lo que tenemos es la fórmula o expresión algebraica de la función.
Fíjate en la siguiente escena. Tenemos una función definida en dos trozos y queremos calcula el límite de la función cuando x tiende a cero. Así que, lo que tenemos que hacer es ir acercándonos a cero, pero claro, podemos hacerlo como ya sabes por la izquierda o por la derecha.
Si lo hacemos por la izquierda, tenemos que coger el primer trozo de función, pues es el que está definido para valores menores que 0. Pulsa sobre el control "x1" que empieza en -1 y vete acercando a cero (aumentando el valor de x1.) Fíjate que los valores de la función, en azul, se van acercando a 1, luego:
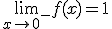
Si nos vamos ahora a la derecha de 0, tenemos que coger el segundo trozo. Si manipulamos ahora el control "x2", vemos que a medida que lo vamos disminuyendo hasta estar muy muy próximo a cero, los valores de la función se acercan a 1. Por tanto,
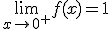
Y como ambos límites laterales coinciden, podemos decir que 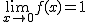
Applet Descartes de José Manuel Gallardo Morilla bajo licencia Creative Commons.
Fíjate ahora en esta otra escena. Volvemos a calcular el límite cuando x tiende a cero, pero si mueves los controles "x1" y "x2" puedes ver que a medida que nos acercamos a cero los valores de la función van creciendo cada vez más, así que, en este caso, diremos que:
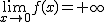
Applet Descartes modificado del original de José Manuel Gallardo Moreno publicado bajo licencia Creative Commons.