2. Cálculo de límites
Regla I
Para calcular el límite de una función, cuando x tiende a x0, basta con sustituir x0 en la función y si nos da un número, es decir, se pueden hacer todas las operaciones, ese es el resultado del límite.
Regla II
En una función a trozos, para calcular el límite en el punto donde se corta la función, hay que hacer los límites laterales y para ello sustituir en los trozos adecuados.
Regla III
Las funciones polinómicas, cuando x tiende a +∞ o -∞, se comportan del mismo modo que su término de mayor grado:
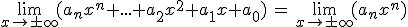
Elige la opción correcta en los límites que aparecen a continuación.
1) 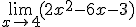
|
-11
| |
|
-7
| |
|
5
|
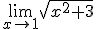
|
2
| |
|
4
| |
|
0
|
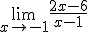
|
0
| |
|
-8
| |
|
4
|
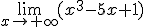
|
+∞
| |
|
-∞
| |
|
No existe
|
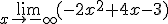
|
+∞
| |
|
-∞
| |
|
0
|
Funciones exponenciales, logarítmicas y trigonométricas
En estas funciones, hay que tener un poco de cuidado al calcular los límites cuando x tiene a infinito. Debes recordar que:
Exponenciales
Si a>1; a+∞ = + ∞ y a-∞ = 0. Por ejemplo, 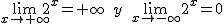 .
.
Si 0<a<1; a+∞ = 0 y a-∞ = + ∞. Por ejemplo, 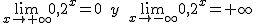
Logarítmicas
Si a>1; loga(+∞) = +∞ y loga(0+) = -∞. Por ejemplo, 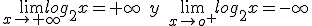
Si 0<a<1; loga(+∞) = -∞ y loga(0+) = +∞. Por ejemplo, 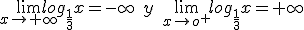
Trigonométricas
No existen los límites cuando x tiende a ±∞ por tratarse de funciones periódicas.