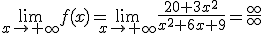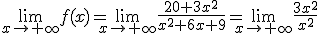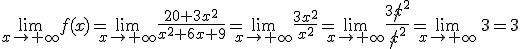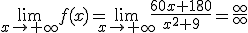2.2. Indeterminaciones con infinitos
INDETERMINACIÓN ∞ / ∞
En el ámbito de las Ciencias Sociales, es muy habitual que haya que calcular el límite de una función racional cuando x tiende a infinito. Basta que queramos saber el comportamiento de una población, del dinero invertido en un banco, de la evolución de un negocio, de la evolución de un mercado de valores, ...., a largo plazo. Muchas de estas funciones responden a funciones racionales, o sea, a dividir dos polinomios, y como ya sabes del punto 2, el resultado del límite cuando x tiende a infinito de un polinomio es infinito. Luego en este caso tendríamos que dividir infinito entre infinito. Tenemos ahora entonces la indeterminación ∞/∞
Seguramente has pensado que eso es 1, si se dividen dos cantidades iguales el resultado es 1. Pero eh ahí el porqué esto es una indeterminación, porque no sabemos si esos infinitos son iguales o uno es mucho más grande que otro. Es decir, hay que averiguar que relación hay entre esos infinitos, y al final, el resultado puede ser efectivamente uno, pero también puede ser cero, infinito o cualquier número real.
Fíjate en los dos ejemplos que aparecen resueltos a continuación:
Ejemplo o ejercicio resuelto
 |
| Imagen de ruurmo bajo licencia Creative Commons. |
El número de individuos, en millones, de una población viene expresada por la función:
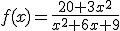
donde x indica el tiempo que va transcurriendo desde este momento. ¿Qué ocurre con esta población a largo plazo? ¿A qué tiende este pueblo, a estabilizarse, a desaparecer o a crecer indefinidamente?
 |
| Imagen de Jerónimo Palacios bajo licencia Creative Commons |
Vemos otro ejemplo:
La siguiente función muestra el número de clientes dispuestos a contratar un producto financiero desde el momento en que se lanza la oferta y sin ningún tipo de publicidad posterior ( x en meses):
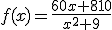
¿Cuántos clientes contratarán ese producto si el tiempo se hace infinitamente grande?
Importante
Para resolver la indeterminación ∞ / ∞, nos quedamos con los términos de mayor grado del numerador y del denominador, simplificamos y volvemos a tomar límite.
- Si el grado del numerador es mayor que el del denominador, el resultado del límite será ±∞.
- Si los grado son iguales, el resultado será el número que resulte de dividir los dos coeficientes.
- Si el grado del denominador es mayor, el resultado será 0.
En este vídeo, se resuelven varios ejemplos de estas indeterminaciones, aunque la forma de hacerlo es un poco distinta. Se dividen todos los términos por la x de mayor grado. Se simplifica y se toma límite, quedando el cociente de dos números, cero entre un número y por tanto cero el resultado o un número entre cero siendo entonces el límite infinito:
Curiosidad
 |
| Imagen de Daquella manera bajo licencia Creative Commons. |
¡OJO! Si estamos haciendo un límite:
- Un número entre 0 es infinito
- Un número entre infinito es 0
- Infinito entre 0 es infinito
- 0 entre infinito es 0
- Infinito entre un número es infinito
- 0 entre un número es 0
AV - Actividad de Espacios en Blanco
=
=
=
=
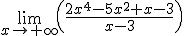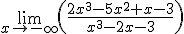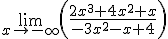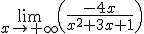Indeterminación ∞ - ∞
Esta indeterminación puede presentarse de varias formas. En principio, si se trata de una resta, es cuestión de comparar grados y ver cuál es mayor:
Ojo, debes tener en cuenta que cuando tomamos valores grandes, una exponencial siempre manda sobre una polinómica y una polinómica siempre manda sobre una logarítmica.
Los casos habituales en los que hay que hacer algo más son en los que aparecen una resta de fracciones y ambas salen infinitos o cuando restamos una función con raíz cuadrada. En este enlace aparecen explicados estos casos.
A continuación te ponemos dos vídeos, uno con fracciones y el otro con raíces:
Curiosidad
ATENCIÓN
∞ - ∞ → Indeterminación
-∞ + ∞ → Indeterminación
∞ + ∞ = +∞
-∞ - ∞ = -∞