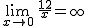2.1. Indeterminaciones
INDETERMINACIÓN K/0
En el apartado anterior, hemos dicho que para calcular el límite de una función en un punto basta con sustituir el valor de x en la función y que si las operaciones se pueden hacer, el resultado obtenido es el del límite. Pero, ¿cuándo no se pueden hacer las operaciones? Pues por ejemplo, cuando estamos haciendo una raíz cuadrada y dentro nos sale un número negativo, cuando hacemos un logaritmo y lo de dentro es cero, o cuando estamos haciendo una división y tenemos que dividir entre cero. Pruébalo, coge una calculadora y divide cualquier número entre 0, ¿qué ocurre? ¿qué te muestra?
Que nada de nada, que no existe, pero claro si lo piensas fríamente es así. ¿Cómo vas a repartir 8 caramelos entre 0 niños? ¿Cómo vas a hacer el reparto si no tienes a quien dárselos?
En este último caso, la operación directa no se puede hacer pero si nos vamos aproximando sí que obtenemos algún resultado. Estos casos son los que se llaman indeterminaciones y en este apartado vamos a ver cómo se resuelven algunos de los tipos más característicos.
Empezamos con este, con el dividir un número entre 0 que en general se conoce o se expresa por indeterminación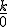 
Ejemplo o ejercicio resuelto
 |
| Imagen de lisibo bajo licencia Creative Commons |
Fíjate en este ejemplo tan tonto para ilustrar lo que ocurre.
Una freidora tiene una capacidad de 12 litros de aceite. Si la llenamos con botellas de a litro, necesitamos 12, si la llenamos con botellas de medio litro, necesitamos 24. Si las botellas son de 20 cl, o sea, 0,2 litros, necesitamos 60 y así, a medida que la capacidad de la botella es menor, más botellas hacen falta.
Si llamamos x, a la capacidad de la botella de aceite (en litros), el número de botellas necesarias vendrá dada por la función:
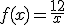
¿Cuántas botellas hacen falta si la capacidad de cada una es muy pero que muy pequeña?
Importante
INDETERMINACIÓN 0/0
Y todavía más raro, ¿puede pasar que también el numerador sea cero? Si un número entre 0 es infinito, ¿0 entre 0 qué será? ¿0? ¿Infinito? ¿1?
Pues esto de cero partido cero sí que es una verdadera indeterminación porque puede ser cualquier cosa. Puede ser 0, puede ser ∞, puede ser 1, puede ser 14, puede ser...
Cuando ocurre esto, tenemos que conseguir simplificar la fracción y para ello hemos de conseguir factorizar los polinomios del numerador y denominador. Si no recuerdas cómo se factorizaba un polinomio, sigue este enlace donde te lo explican todo paso a paso:
Una vez hecho esto y simplificada la expresión, la indeterminación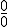 
habrá desaparecido y se podrá calcular el límite.
Te enseñamos cómo hacerlo en los siguientes vídeos. En el primero sale 1,5 y en el segundo infinito, pues al resolverlo, vamos a parar ahora al caso k/0:
|
|
|
Para saber más
Esto se puede complicar todo lo que se quiera. Según cómo sea la función, el límite es más fácil o más complicado de calcular.
En el siguiente vídeo, se muestra cómo se resuelve una indeterminación 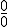cuando en el numerador o denominador de la fracción hay algún término dentro de una raíz cuadrada y otra cantidad sumando o restando fuera.
AV - Actividad de Espacios en Blanco
Calcula el valor de los siguientes límites. En caso de que alguno sea infinito, escribe el signo y a continuación sin dejar espacio en blanco I. Por ejemplo, si quieres escribir -∞, has de teclear "-I"
Si el resultado sale una fracción, utiliza la barra inclinada para separar. Por ejemplo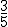 
escríbelo así: 3/5
=
=
=
=
=
=
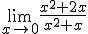
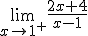
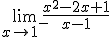
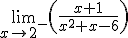
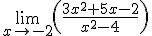
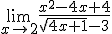