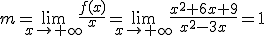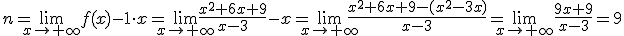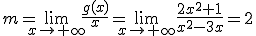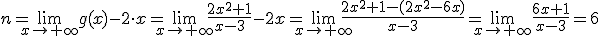3. Asíntotas y ramas infinitas
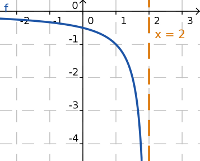
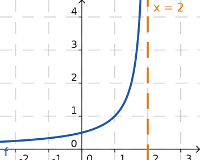
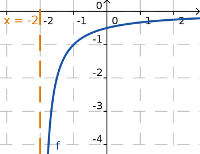
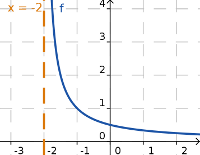
Sea a un número real, la recta vertical x=a es una asíntota vertical de la función y=f(x) si se verifica alguna de las siguientes propiedades:
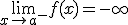 |
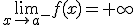 |
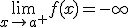 |
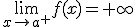 |
 |
 |
|
 |
¿Cómo saber donde buscar la asíntota vertical?
- Si es una función polinómica, no tiene asíntotas de ningún tipo.
- Si es una función RACIONAL, tendremos que buscar en las raíces del denominador, o lo que es lo mismo, donde se anula el denominador. Eso son los candidatos; después hay que comprobar que efectivamente es así.
Ejemplo:
Si tenemos la función 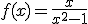 y queremos calcular sus asíntotas verticales, tendremos que estudiar para que valores x2-1=0. En este caso las posibles asíntotas verticales son x=1 y x=-1.
y queremos calcular sus asíntotas verticales, tendremos que estudiar para que valores x2-1=0. En este caso las posibles asíntotas verticales son x=1 y x=-1.
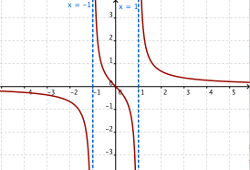 |
x=1. Tenemos que calcular el límite cuando x=1- y el límite cuando x=1+.
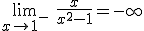 (Basta ver el signo del O) La
asíntota vertical es como la primera imagen de la definición.
Cuando nos acercamos a x=1 por la izquierda la gráfica de f(x) tiende a
-∞.
(Basta ver el signo del O) La
asíntota vertical es como la primera imagen de la definición.
Cuando nos acercamos a x=1 por la izquierda la gráfica de f(x) tiende a
-∞.
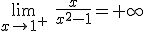 La
asíntota vertical es como la última imagen de la definición.
Cuando nos acercamos a x=1 por la derecha la gráfica de f(x) tiende a
+∞.
La
asíntota vertical es como la última imagen de la definición.
Cuando nos acercamos a x=1 por la derecha la gráfica de f(x) tiende a
+∞.
x=-1. Tenemos que calcular el límite cuando x=-1- y el límite cuando x=-1+.
En este caso 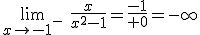 . Estamos en el caso 2 de la definición. Cuando nos acercamos a x=-1 por la izquierda la gráfica de f(x) tiende a -∞.
. Estamos en el caso 2 de la definición. Cuando nos acercamos a x=-1 por la izquierda la gráfica de f(x) tiende a -∞.
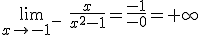 ,
esto es, es similar a la tercera gráfica de la definición. Cuando nos
acercamos a x=-1 por la derecha, la gráfica de f(x) tiende a
+∞.
,
esto es, es similar a la tercera gráfica de la definición. Cuando nos
acercamos a x=-1 por la derecha, la gráfica de f(x) tiende a
+∞.
- Otra función que tiene asíntota vertical es la función LOGARÍTMICA, más concretamente, en los puntos extremos de los intervalos donde empieza el dominio.
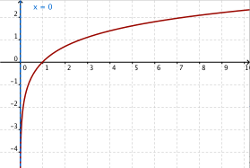
| y=ln(x) |
|
|
|
El logaritmo tiene una asíntota vertical x=0; donde empieza o termina el dominio
|
Calcula, si las tienen, las asíntotas verticales de las siguientes funciones:
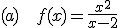 |
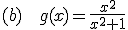 |
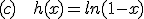 |
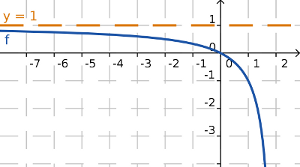
Sea b un número real, la recta horizontal y=b es una asíntota horizontal de la función y=f(x) si se verifica alguno de los siguientes límites:
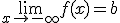 |
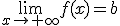 |
 |
|
Calcula, si las tienen, las asíntotas horizontales de las siguientes funciones:
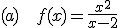
|
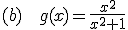 |
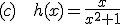
|
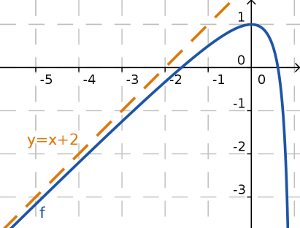
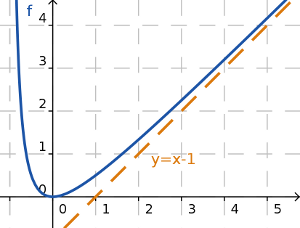
La recta y=mx+n, m≠0 es una asíntota oblicua de y=f(x) si se verifica alguno de estos límites:
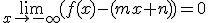 |
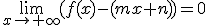 |
|
|
Para calcular la ecuación de la asíntota, y=mx+n, tendremos que calcular: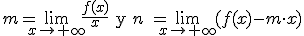
Calcula la asíntota oblicua de las siguientes funciones:
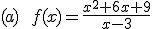
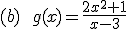
Aquí te dejo dos vídeos para que veas paso a paso cómo se hallan las asíntotas de una función racional:
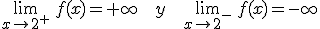 . Por lo tanto, tiene una asíntota vertical en x=2.
. Por lo tanto, tiene una asíntota vertical en x=2.
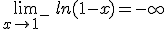 .
.
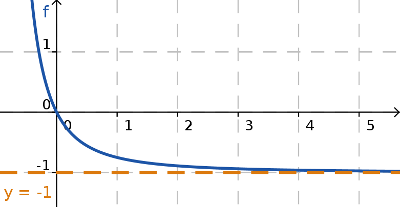
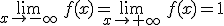 . Esto quiere decir que la asíntota horizontal es y=1.
. Esto quiere decir que la asíntota horizontal es y=1.
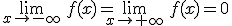 . Esto quiere decir que la asíntota horizontal es y=0.
. Esto quiere decir que la asíntota horizontal es y=0.