2.1 Propiedades de los determinantes
Curiosidad
PROPIEDADES DE LOS DETERMINANTES
- |A| = |At|
- Si los elementos de una fila o columna se multiplican por un número, el determinante queda multiplicado por dicho número.
- Si k es un número real y A una matriz cuadrada de orden "n", |k·A| = kn·|A|, es decir, si multiplicamos una matriz por un número, el determinado queda multiplicado por el número levado al tamaño de la matriz. (Ten en cuenta que por cada fila que se multiplique, sale una vez del determinante)
- Si los elementos de una línea se pueden descomponer en dos sumandos, el determinante se puede separar en suma de dos, dejando el resto de líneas igual y separando los sumandos en la fila o columna afectada.
- |A · B| = |A| · |B|
- Si se cambian dos líneas de orden, el determinante cambia de signo.
- Si hay dos líneas iguales o proporcionales, el determinante es cero.
- Si una línea se obtiene como combinación lineal de otras, el determinante es cero.
- Si una línea se cambia por ella más una combinación lineal de otras, el determinante no varía.
Ejemplo o ejercicio resuelto
Aquí te presentamos un ejercicio en que se calculan determinantes a partir de las propiedades de estos:
En este otro, comprobamos que el determinante es cero haciendo que dos filas sean iguales. ¿Cómo? Multiplicando la primera fila por una cantidad:
Importante
ELEMENTO ADJUNTO Y MATRIZ ADJUNTA
Dada una matriz A, se llama elemento adjunto del elemento de la matriz aij, y se representa por Aij al número que resulta de aplicar la fórmula:
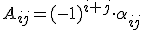
donde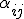 
representa el determinante que queda de quitar de la matriz A la fila "i" y la columna "j".
En el siguiente vídeo tienes un ejemplo:
La matriz que resulta de calcular todos los elementos adjuntos se llama matriz adjunta y se representa por Adj(A).
Para saber más
DESARROLLO DE UN DETERMINANTE POR UNA FILA O COLUMNA
A veces es interesante o incluso más cómodo calcular un determinante utilizando los adjuntos y lo que se llama el desarrollo por una fila o columna. Además, utilizando esto, podríamos calcular cualquier determinante, sea del tamaño que sea: 4x4, 5x5, ...
A continuación te ponemos dos vídeos para ver cómo se hace esto en matrices de orden 3. Si quieres hazlo por la regla de Sarrus y comprueba que efectivamente, el resultado es el mismo: