Dos rectas en el espacio se cruzan, se cortan en un punto, son paralelas o son coincidentes. Los casos se pueden distinguir a partir de las ecuaciones implícitas o usando los puntos o vectores.

A través de las ecuaciones implícitas se ve con los rangos de las matrices de coeficiente y ampliada:

• 2-2→ Coincidentes.
• 2-3→ Paralelas.
• 3-3→ Se cortan en un punto; el que sale de resolver el sistema.
• 3-4→ Se cruzan.

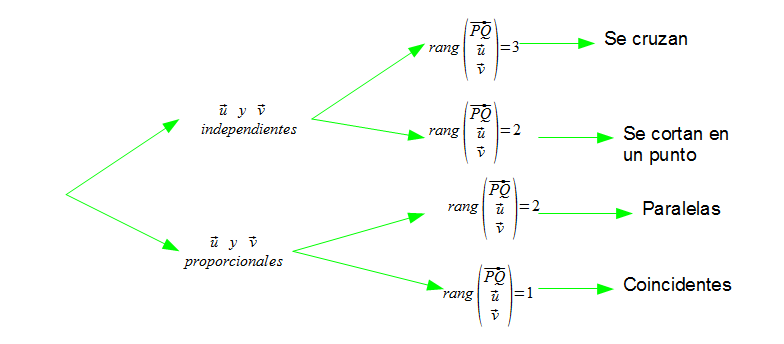
Con los puntos y vectores se comparan los vectores de las rectas y los puntos siguiendo este esquema: