2. Ecuaciones de un plano
Actividad
Para expresar la ecuación de un plano necesitamos un punto por el que pase y dos vectores que indiquen dos direcciones distintas de éste, es decir, dos vectores linealmente independientes.
Si el punto es P=(x0,y0, z0) y los vectores son u=(u1, u2, u3) y v=(v1,v2,v3), las ecuaciones son:
Ecuación vectorial: (x,y,z) = (x0,y0, z0) + λ(u1, u2, u3) + μ(v1,v2,v3)
Ecuación paramétrica: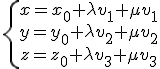 
Ecuación Implícita: Ax + By + Cz + D = 0
Caso de estudio
Ecuación de un plano que pasa por tres puntos
Pasar de paramétrica a implícita
Pasar de Implícita a Paramétrica
Ecuación de un plano que contiene a un punto y a una recta
Ecuación de un plano que contiene a una recta y es paralelo a otra
Cogemos punto y vector de la recta contenida y el vector de la que es paralelo, pues si una recta es paralela a un plano, el vector director de esta, también será vector director del plano.