Geometría métrica. Matemáticas II
7. Esquemas y ejercicios
Trucos a tener en cuenta
- Si una recta es paralela a un plano, el vector director de la recta es uno de los vectores directores del plano.
- Si una recta es paralela a un plano, el producto escalar del vector de la recta con el vector normal del plano es cero, pues son perpendiculares.
- Si una recta es perpendicular a un plano, el vector director de la recta es el normal del plano.
- Si dos planos son perpendiculares, el vector normal de uno es director del otro.
- Si nos piden calcular el punto sobre una recta que cumpla una condición, suele ser buena idea pasar la recta a forma paramétrica y tener así las tres coordenadas del punto dependiendo únicamente de un parámetro, λ.
- Si un plano es mediatriz de un segmento, todos los puntos del plano están a igual distancia de los extremos del segmento y es perpendicular al segmento pasando por el punto medio.
- Equidista es lo mismo que igual distancia.
- Para hacer una recta perpendicular a otra, unimos el punto por el que tiene que pasar con la proyección de éste sobre la recta.
- Si una recta es paralela a un plano, el producto escalar del vector director de la recta y el normal del plano es 0.
- Si una recta es perpendicular a un plano, el producto vectorial del vector director de la recta y el normal del plano es
.
Para practicar
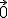Para terminar, un esquema con lo más importante del tema y ejercicios con sus soluciones para que practiques todo lo que hemos visto en estos dos temas de geometría métrica: Ángulos, cortes, áreas, distancias, ...
Bajo Licencia Creative Commons Attribution 3.0 License
Temas 6 y 7: Geometría euclídea y métrica. Matemáticas II.