1. Producto escalar
Importante
Como recordarás del curso pasado, el producto escalar de dos vectores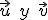 
se definía así:
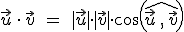
Es decir, el producto de los módulos de los vectores por el coseno del ángulo que forma estos. Como puedes observar, el producto escalar es una operación entre vectores cuyo resultado es un escalar, es decir, un número real.
Si conocemos las coordenadas de los vectores respecto a la base canónica, todo esto es más simple, pues se reduce a multiplicar componente a componente y sumar:
Si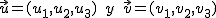 
→ 
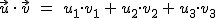
Lo vemos en el vídeo:
Propiedad del producto escalar
Si dos vectores son perpendiculares u ortogonales (también se llama así) el producto escalar ha de ser cero, pues si recuerdas el coseno de 90º era cero. Y viceversa, si el producto escalar es cero, ha de ser forzosamente porque ambos vectores sean perpendiculares, luego:
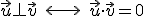
En el siguiente vídeo, resolvemos una cuestión sobre vectores perpendiculares:
Importante
El vector normal del plano es el único vector (salvo vectores proporcionales) perpendicular a todos los vectores del plano. Se suele representar con la letras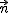 
Si conocemos la ecuación implícita del plano, el vector normal viene dado por los coeficientes de x, y, z en dicha ecuación:
Π: Ax + By + Cz + D = 0 →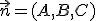 
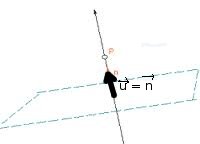
Curiosidad
- Con el vector normal y un punto por el que pase, puede determinarse la ecuación implícita de un plano.
- Si una recta es perpendicular a un plano, el vector director de la recta es el vector normal del plano.
- Si dos planos son paralelos, tienen el mismo vector normal, por lo que su ecuación implícita sólo variará en el término independiente D.
Bajo Licencia Creative Commons Attribution 3.0 License
Temas 6 y 7: Geometría euclídea y métrica. Matemáticas II.