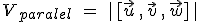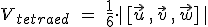4. Producto mixto
 |
| Imagen de Horacio LledAas bajo licencia Creative Commons |
Una nueva operación entre vectores, con la diferencia de que ahora manejamos tres, es la que llamamos producto mixto. El nombre se debe a que ponemos en juego a la vez, el producto escalar y vectorial de vectores.
El producto mixto de tres vectores, que expresaremos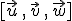 
, se define como el producto escalar del primero por el resultado del producto vectorial de los otros dos. El resultado, por tanto, será un número o escalar.
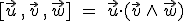
En realidad, y puesto que nuestros vectores están referidos a la base canónica, esta operación conjunta equivale a calcular el determinante de la matriz que forman los tres vectores:
Propiedades del producto mixto
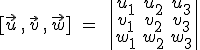
- Si cambiamos de orden los vectores, el producto mixto cambia de signo, salvo que hagamos un cambio cíclico, en el que el signo se mantendrá pues equivale a hacer dos cambios ordinarios:
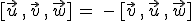
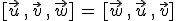
- El producto mixto de tres vectores es nulo si, y sólo si, los tres vectores son linealmente dependientes, o lo que es lo mismo, los tres vectores están incluidos en un plano o son coplanarios.
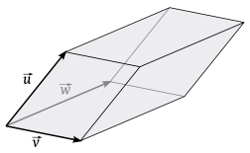
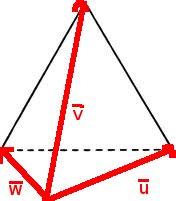
- Interpretación geométrica: El valor absoluto del producto mixto de tres vectores nos da el volumen del paralelepípedo que genera las aristas de esos tres vectores. Además, puesto que el tetraedro que tiene de aristas esos tres vectores es la sexta parte del paralelepípedo, el volumen del tetraedro será el producto mixto entre seis:
 |
|
 |
|
En los siguientes vídeos tienes dos ejercicios resueltos para calcular el volumen de un paralelepípedo o de un tetraedro:
| Volumen de un paralelepípedo |
Volumen de un tetraedro |
Bajo Licencia Creative Commons Attribution 3.0 License
Temas 6 y 7: Geometría euclídea y métrica. Matemáticas II.