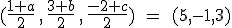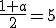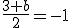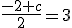3.1. Simétricos
¡Recuerda!
 |
| Imagen de arturomandly bajo licencia Creative Commons |
Si tenemos dos puntos A y B, el punto medio del segmento se calcularía sumando al punto A, la mitad del vector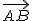 
. Pero como ya bien sabes no se pueden sumar puntos y vectores, sino vectores.
Como las coordenadas del punto A coincide con las coordenadas del vector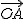 
para calcular el punto medio, procedemos así:
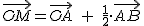
Pero en realidad, esa operación equivale a sumar componente a componente las coordenadas de los puntos y dividirlas entre dos, es decir:
Observa
 |
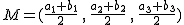
| Imagen de Pablo Maro bajo licencia Creative Commons |
Simétrico de un punto respecto a otro
El simétrico de un punto P respecto a otro punto Q, será un punto, que podemos llamar Ps, y que debe cumplir que el punto medio del segmento PPs sea Q.
Por ejemplo, P= (1, 3, -2) y Q= ( 5, -1, 3), ¿cuál es el simétrico de P respecto de Q?
Aprende a hacerlo
En el vídeo puedes ver resuelto un ejercicio de calcular el simétrico de un punto respecto a un plano:
Simétrico de un punto respecto a una recta
En el vídeo, tienes un ejemplo resuelto:
Recta simétrica de una respecto a un plano
Para esto, calculamos dos puntos de la recta y hayamos sus simétricos respecto al plano. La recta que une los puntos simétricos será la recta simétrica respecto al plano.
Bajo Licencia Creative Commons Attribution 3.0 License
Temas 6 y 7: Geometría euclídea y métrica. Matemáticas II.