Perpendicular común a dos rectas que se cruzan

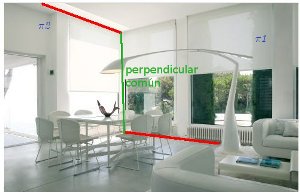Si dos rectas r y s se cruzan, hay una recta que es simultáneamente perpendicular a ambas, y además, el corte de esta con las rectas originales nos dan los puntos más próximos entre las rectas. Procedemos así:

1. Calculamos el producto vectorial, que llamaremos 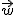de los vectores directores de r y s. Este vector será perpendicular a la vez a r y s.
2. Hallamos el plano π_r que contiene a la recta r y al vector .
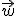3. Hallamos el plano π_s que contiene a la recta s y al vector .
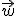4. La recta que sale de cortar ambos planos (juntar las dos ecuaciones implícitas) es la perpendicular común buscada pues el plano π_r es perpendicular a s y el plano π_s es perpendicular a a r.

Nota: Si las rectas se cortan, también podemos calcular la perpendicular común siguiendo estos pasos, aunque bastaría con hacer la recta que lleva como dirección el producto vectorial de los vectores directores y que pasa por el punto de corte de las rectas.

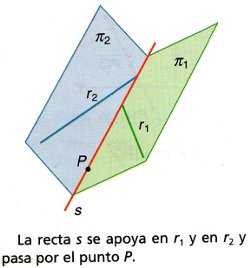
Recta que se apoya en dos y pasa por un punto dado

Tenemos dos rectas r₁ y r₂ y queremos calcular otra que pasa por un punto P y toca a las otras dos. Procedemos así:

1. Calculamos el plano π₁ que contiene a r₁ y al punto P.
2. Calculamos el plano π₂ que contiene a r₂ y al punto P.
3. La recta s que sale de cortar ambos planos (juntar las dos ecuaciones implícitas) es la solución buscada.

Recta que se apoya en dos y es paralela a una tercera

El procedimiento es exactamente igual que el anterior cambiando la condición de que contiene al punto P a que los planos han de contener al vector de dirección de la tercera recta. Tenemos pues dos rectas r₁ y r₂ y queremos calcular otra que es paralela a una tercera recta s y toca a las otras dos. Procedemos así:

1. Calculamos el plano π₁ que contiene a r₁ y es paralelo a la recta s.
2. Calculamos el plano π₂ que contiene a r₂ y es paralelo a la recta s.
3. La recta que sale de cortar ambos planos (juntar las dos ecuaciones implícitas) es la solución buscada.