Imagen de Olga Díez (caliope) bajo licencia Creative Commons

Distancia entre dos puntos

Simplemente hay que hacer el módulo del vector que une los puntos:

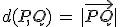
Distancia de un punto a un plano

Como distancia, consideramos la más pequeña, es decir, la distancia del punto al punto del plano más próximo a él, y ese justamente, es el que cae sobre la perpendicular, o sea, la proyección del punto sobre el plano. Luego podríamos calcular la proyección del punto sobre el plano y a continuación la distancia entre los dos puntos.

Pero esa operación, si el punto es P=(x₀, y₀, z₀) y el plano es π: Ax + By + Cz + D = 0,  es equivalente a aplicar la fórmula:

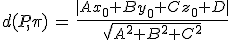
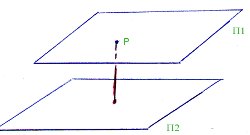Distancia entre dos planos

En el caso de que dos planos sean paralelos, calcular la distancias entre ellos es muy simple, pues sólo tenemos que coger un punto de uno de los planos y calcular la distancia de éste al otro plano, aplicando la fórmula anterior.

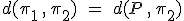
Si los planos no son paralelos, no hay nada que hacer, pues los planos tendrán puntos en común y por tanto, la distancia será cero.

Distancia de un punto a una recta

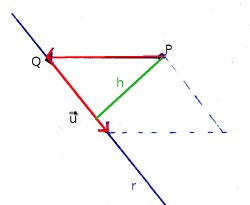Igual que con la distancia de un punto a un plano, podríamos calcular esta distancia hayando previamente la proyección del punto P a la recta r y después calcular la distancia dl punto a su proyección, pero vamos a buscar una forma más cómoda y rápida de hacer esto.

Suponemos que de la recta r, conocemos un punto Q y el vector director 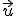. Entonces, fíjate que podemos formar un paralelogramo como el de la derecha cuyos lados son los vectores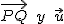

Como hemos visto en el punto 2 del tema, el área del paralelogramo se calculaba con el módulo del producto vectorial de los vectores que formaban sus lados, en este caso, el área sería 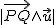. Pero de siempre, el área de un paralelogramo se calculaba como base por altura, y se te fijas en éste, la longitud de la base es el módulo del vector 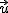y la altura h sería precisamente la distancia del punto a la recta, luego despejando, obtenemos la fórmula que vamos a utilizar:

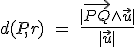
A continuación, algunos ejemplos resueltos: