Geometría métrica. Matemáticas II
2. Producto vectorial
El producto vectorial de dos vectores 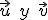 , que expresamos de la forma
, que expresamos de la forma 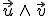 , es el vector que se obtiene desarrollando el determinante:
, es el vector que se obtiene desarrollando el determinante:
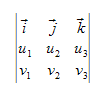
En el siguiente vídeo, puedes ver un ejemplo.
 |
| Imagen de Luciti bajo licencia Creative Commons |
- El módulo del producto vectorial, viene dado por la fórmula:
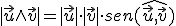
- El resultado del producto vectorial, es un vector perpendicular a la vez a
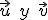 .
.
- Si los vectores
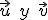 son paralelos (proporcionales), el producto vectorial es el vector nulo (0,0,0), y recíprocamente, si el producto vectorial es cero, es porque los vectores son paralelos.
son paralelos (proporcionales), el producto vectorial es el vector nulo (0,0,0), y recíprocamente, si el producto vectorial es cero, es porque los vectores son paralelos.
- Interpretación geométrica:
 El módulo del producto vectorial es el área del paralelogramo que tiene por lado dichos vectores:
El módulo del producto vectorial es el área del paralelogramo que tiene por lado dichos vectores:
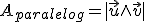
Por tanto, el área de un triángulo puede calcularse dividiendo el módulo del producto vectorial de los vectores que forman dos lados entre 2, pues el triángulo ocupa la mitad del paralelogramo.
- Si tenemos la ecuación implícita de una recta y queremos averiguar su vector director, el producto vectorial de los vectores normales de los planos que forman esa ecuación nos lo da, pues la recta es perpendicular a los dos vectores normales
| Área de un paralelogramo |
Área de un triángulo |
Bajo Licencia Creative Commons Attribution 3.0 License
Temas 6 y 7: Geometría euclídea y métrica. Matemáticas II.