Cuando hablamos de proyectar, lo hacemos siempre perpendicularmente, es decir, se trata de trasladar un elemento sobre otro de forma que el movimiento que haga sea perpendicular respecto al que estamos trasladando.

En este curso vemos tres tipos de proyecciones, de un punto sobre un plano, de un punto sobre una recta y de una recta sobre un plano.

 

Proyección de un punto sobre un plano

 

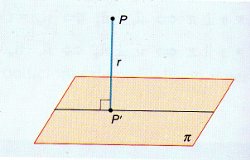
Calculamos la recta perpendicular al plano π que pasa por el punto P.

Cortamos la recta obtenida con el plano (ya sabes, sustituir la paramétrica de la recta en la implícita del plano).

El punto de corte obtenido, es la proyección P' del punto P sobre el plano π.

 

 

 

Proyección de un punto sobre una recta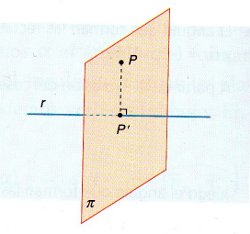

 

Calculamos el plano perpendicular a la recta r que pasa por P

 

Cortamos recta y plano. El punto obtenido P', es la proyección del punto P sobre la recta r

 

 

 

 

 

Proyección de una recta sobre un plano

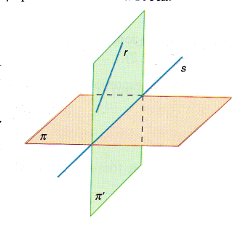Podemos hacerlo de dos formas:

Forma 1: Cogemos dos puntos de la recta P y Q y hacemos la proyección de estos sobre el plano, obteniendo así dos puntos en el plano P' y Q'. La recta que une estos puntos es la proyección de la recta r sobre el plano π.

Forma 2: 

Calculamos el plano π' perpendicular a π y que contiene a r

La recta s que se obtiene al cortar los planos π y π', es la proyección de r sobre π.