4. Integrales de funciones racionales

Funciones racionales son las que se  forman como cociente de dos polinomios, por tanto, estamos hablando de integrales de la forma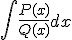

Antes de hacer nada, debemos tener en cuenta dos cosas:

• Si el grado del numerador es mayor o igual que el del denominador, debemos hacer la división de los polinomios, calculando el cociente y el resto. Hecho esto, y aplicando la regla de la división (dividendo=cociente · divisor + resto), hacemos la siguiente descomposición:

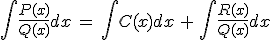
Observa que la primera integral, la sabemos hacer sin problemas pues es la integral de un polinomio, y la segunda, es la integral de una función racional en la que el grado del numerador es menor que el del denominador.

• Si en el numerador aparece la derivada del denominador, la integral será logaritmo neperiano del denominador, pues podría resolverse mediante un cambio de variable llamando "t" al denominador.

Una vez que el grado del numerador es menor que el del denominador y la integral no se puede resolver por cambio de variable, tenemos que recurrir a descomponer en raíces el denominador y en descomponer la función en suma de fracciones simples. Según como sean las raíces del polinomio del denominador distinguimos estos tres casos:

1. El denominador solo tiene raíces reales simples.
2. El denominador solo tiene raíces reales y alguna de ellas múltiple.
3. En el denominador aparece alguna raíz compleja.