6. Área de un recinto limitado por una curva
Importante
Como puedes ver, para determinar el área del recinto limitado por la gráfica de una función, el eje OX y las rectas x=a y x=b, calculamos la integral definida de la función en el intervalo [a,b].

Pero claro, si la función es negativa, es decir, está por debajo del eje de abscisa y hacemos la integral definida, el resultado que nos da es negativo. Y un área negativo, no tiene mucho sentido, ¿verdad?
¿Cómo lo arreglamos? Pues fácil, poniéndole un signo menos delante a la integral:
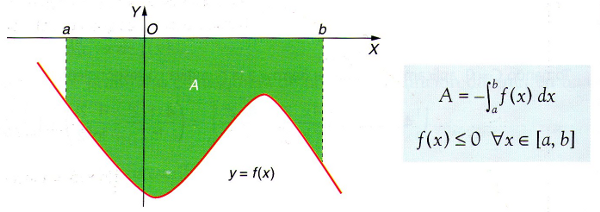
Claro que esto tiene un problema, si no tenemos la gráfica por delante, tenemos que ver previamente el signo de la integral. Pues bien, para evitar esto, y generalizar el resultado, podemos meter la integral entre valor absoluto y así me da positivo. Por tanto,

Otro problema es que la función atraviese el eje OX en medio del intervalo, o sea, que se distingan dos trozos. Pues bien, en este caso, lo que hemos de hacer es partir también la integral y hacerla de cada uno de los trozos, como por ejemplo, en la imagen inferior:
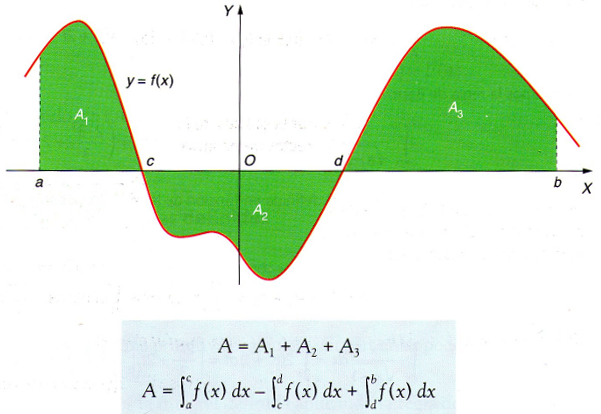
Caso de estudio
Dos vídeos con ejemplos resueltos. Observa que lo fundamental es ver si entre los valores de x que me dan, la función atraviesa o no el eje OX, para separar o no la integral en varias partes. Es conveniente hacer el dibujo para aclarar la idea del área que tenemos que calcular y desde dónde hasta dónde van las integrales, pero no es absolutamente necesario.